Koliko sisa je dovoljno sisa, matematički gledano?
Uradi ovaj test i saznaj koliko dobro poznaješ brojke koje su promenile istoriju čovečanstva.
Loading ...
Loading ...
Loading ...
Loading ...
Loading ...
Loading ...
Loading ...
a)
Ako i jeste rezolucija nismo je koristili, a Sveti Sava se rodio malko ranije. 800×600 forevr. Reč je, naravno, o broju koji Žika Todorović svečano navodi u filmu “Mi nismo anđeli” kao broj sukanja koje je za života zadigao [highlight]Nikola Kojo[/highlight]. 1286 – životni cilj svakog koga poznajem.
b)
Kako se kajmak pravi i koliko mu za to treba nismo upoznati. Što se ispisnica tiče, pu-pu bile ti zanimljive dok si živ. 42 je dakako [highlight]odgovor na sve[/highlight] jednog super-kompjutera. Pitanjem “Koji je odgovor na ultimativno pitanje života, univerzuma i svega” Douglas Adams u delu “Autostoperski vodič kroz galaksiju” ismeva ljudsku radoznalost i primorava nas da se suočimo sa činjenicom da možda beskonačnost naše potrage za odgovorima ne leži u njihovom nepostojanju – već u nevešto postavljenim pitanjima. Za preporučiti je i Adamsova knjiga “Put na Mars” u kojoj ekspanziju kosmosa vidi i objašnjava kao puku ironizaciju našeg interesovanja za isto.
c)
Zamalo Bond, ali smo slagali za zadnje dve cifre – falilo bi ti 10 dinara za ovaj broj pakli cigara, ali recimo da imaš i 10 kasirki u kraju koje ti idu na kurac jer ti uvek prosipaju kusur po pultu. Njih 10, a planiraš da živiš još recimo 40 godina. 40×365+10(bonus iz 10 prestupnih godina u 40)=14.610. Puta deset kasirki, imamo 146.100 pakli cigara da zagorčamo svaki jebeni dan svakoj jebenoj kasirki do kraja života kad joj prospemo 130 kovanica na pult. Suvišno je reći, i dalje imamo previše kovanica… Tako da ne, pošto je broj u startu bio pogrešan, cigare nisu tačan odgovor, već [highlight]Pi[/highlight]. 10.000.000.000.000 je najviši broj cifara u broju Pi koje je čovečanstvo do sada uspelo da identifikuje a na toj pobedi 2011. godine imamo da zahvalimo gospodi Shigeru Kondo i Alexander Yee. Najviši broj imenovanih cifara u 2002. godini iznosio je 1.241.100.000.000 i za taj broj je rečeno da, kada bi ga upisali u knjigu, ona bi bila široka koliko je Ajfelov Toranj visok, a da ga izgovorimo naglas – koštalo bi nas 40.000 godina.
d)
Ne, naravno da je Kum samo jedan. Dvojka i trojka nisu opcija, a što se rezultata tvog testa tiče, na pitanje šta je 3 odgovor nije ni broj prstiju neophodnih da bude hetero Srbin, jer je taj broj dva (ako me razumeš). [highlight]Ženke[/highlight] dolaze u različitim težinama i dimenzijama, i naravno da će broj varirati, ali u proseku su tri pića zakon kad ‘oćeš da vodiš kući. Ako se prepije, ‘oće da zažali.
e)
E ovo je broj. 43 kvintiliona načina da se složi originalna 3×3 [highlight]Rubikova kocka[/highlight].
f)
Ni liker koji drži do sebe ne bi dozvolio da ima 14% alkohola. Pelinkovac je svedok. Takođe, Milka Canić nema niti jedan nalog na twitteru, a i da ga ima, šta bi nam pa rekla. U Srbiji je, naime, dozvoljeno imati [highlight]seksualni odnos sa četrnaestogodišnjacima[/highlight] uz uslov pristanka i dobre volje. Znači, ne smeju da idu u Segedin u pazar sami, ne smeju da piju pivo, ali smeju da se driluju u rč. Ipak imaju 14 godina. No, zakon jedne zemlje koji ti za ubistvo da maksimalno 8 godina, pa te posle četiri puste, možda i nije zakon na koji se treba oslanjati. Radi kako se uvek radilo: nek’ priča ona šta ‘oće, a ti se čuvaj ćaće i braće. I odgovor je da, Kim Kardashian na ovoj slici ima 14 godina.
g)
Ovaj broj je toliko velik da to nije istina. 1,956 puta 10 na 1.834.097.-u, to ne može ni da se zapiše. Reč je o konceptualnom razmišljanju Jorgea Luisa Borgesa u njegovoj kratkoj priči [highlight]”Vavilonska Biblioteka”[/highlight]. A biblioteka je takva da sadrži sve moguće knjige. “Sve moguće”? Koncept poznat iz srpskog jezika? Ni blizu. Sve knjige vavilonske biblioteke imaju po 410 strana i 80 redova na svakoj strani. Sve su napisane koristeći 25 slova alfabeta i sve zajedno – sadrže sve kombinacije tih slova u okvirima jednog toma, pri čemu Borhes tvrdi da svaka od knjiga na nekom (što poznatom, što nepoznatom) jeziku – rezultira smislom. Cela knjiga sadržaja “aaaaaaaaaaaaaa…” – postoji. I za nekoga nosi značenje. Isto tako, postoji i knjiga “aaaaaaaa…” koja negde ima jedno skriveno “B”, i ona je sasvim druga knjiga. Da bismo vam bliže predstavili ukupan broj knjiga, razmislite za kraj o nešto preglednijem broju knjiga. Uzmimo jednu knjigu i pretpostavimo da je druga knjiga, u kojoj je negde neko slovo drugačije, knjiga sa greškom u odnosu na prvu. Ukupno bi “varijanata” jedne knjige postojalo:
- Sa jednom greškom:
= 31,488,000 - Sa dve greške:
= 495,746,694,144,000 - Sa tri greške:
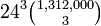= 5,203,349,369,788,317,696,000 - Sa četiri greške:
= 40,960,672,578,684,980,713,193,472,000
Bio je ovo Vehbija sa brojevima koji će vam silovati um i ostaviti ga u jarku da plače, a sve pod maskom lake zabave i testa ličnosti. Raporta i rezultata nema, ako nisi znao odgovore sad znaš, a ako si znao bar četiri – jebeš mnogo dobro. Radostan vam ostatak dana, a što se pitanja iz naslova tiče – shodno odgovoru pod a) dovoljan broj sisa je
1286 x 2 = 2572
