Teorija igara 1 – razuzdana samarićanka, spid, kokain i guslarsko veče
Samo u 2015. godini priča o teoriji igara se zaverglala u svetu čak dva puta. Prvi put kad se Siriza dokopala vlasti u Grčkoj pa se pročulo da je Janis Varufakis ćaća za tu oblast (joooj jesam ja verna mužu i sve to, al bih brate jebala ovog Janisa, vidi ga samo kako se oblači, kako vozi motor, kako je levičar, kako ima teoriju igara u malom prstu, a gde je mali prst, tu je, bome, i srednji – vikaše tada silne žene), i nažalost, kad je jedan od velikih mesija teorije igara, Džon Neš trgično nastradao u saobraćajnoj nezgodi (a brate, gledo sam ja film o Džonu Nešu, kako je samo lud bio, a igra ga mnogo dobro Rasel Krou, kakav glumac, glumi ludaka a zapravo nije lud u stvarnom životu, ma haos – vikaše tad silni muškarci).

Inače je priča o teoriji igara nešto starija; nerafinisana i neintegrisana verzija minimaks pravila potiče još s početka 18. veka, ali teorija igara svoju celovitost dobija u prvoj polovini prošlog veka, tek kad se cele materije dohvatio Džon fon Nojman. Kasnije ju se dorađivali, proširivali, gletovali i hoblovali brojni matematičari (među njima pre svega Oskar Morgenštern i Džon Neš, dobitnik Nobelove nagrade ’94.) pa tako teorija igara danas smatra za jednu od najkorisnijih alatki u svetu donošenju odluka, od ekonomije, vojne strategije i politike do odvlačenja željene osobe u krevet.
Dakle, igre su svuda oko nas a mi se time nismo na višem nivou od profanog do pre nekoliko decenija, što je zabrinjavajuće. Bilo da je u pitanju ajnc, poker, čoveče ne ljuti se, monopol, cenkanje sa grčkim prodavcem u Kateriniju, mimoilaženje sa osobom koja dolazi iz drugog pravca na uskom putu, pregovor sa majstorom oko datuma završetka radova i frekvencije isplate, sve je to igra u kojoj se može ostvariti preimućstvo optimizacijom strategije u datim uslovima i poznavanjem psihologije onog preko puta. Otuda verovatno i fotke prirode sa natpisima – život je igra zato proživi igrajući se i nemoj nikad da odrasteš, koje besomučno po fejsu šeruju ocvale udavače, mastermajndovi teorije igara. Nema drugog zaključka.
Pre započinjanja igranja, treba pomenuti dva bitna činioca koji se često pojavljuju u pravilima igara, a koje zli ekonomski (pleonazam) eksperti (oksimoron) često rabe – Nešov ekvilibrijum i Pareto optimum. Nešov ekvilibrijum mu dođe svaka situacija u kojoj igrači znaju strategije svojih takmaca i gde unilateralna promena strategije jednog ne može da mu donese veći dobitak. Pareto optimum kaže da nikom ne može biti bolje a da drugom ne bude lošije (bejzik ideja komunizma, jelte).
Proste i mešovite matrične igre (igre nulte sume) su zanimljive samo sa matematičko-teorijskog stanovišta, a pošto je Tarzanija sajt koji se bavi više analizom destilata voća i Bobanovom lajt motiv željom – Maja u krevetu, zanemarićemo teoriju minimaksa (ne pokojnog Miće) i spektralnu analizu igre par-nepar i ostaviti je studentima primenjene matematike a mi ćemo se ovde baviti konkretnom primenom igara u ćivotu, te sa menija prvo uzimamo predjelo u vidu nečega što ne zvuči ukusno kao njeguški pršut sa kajmakom, verovatno zato jer se zove igra koordinacije.
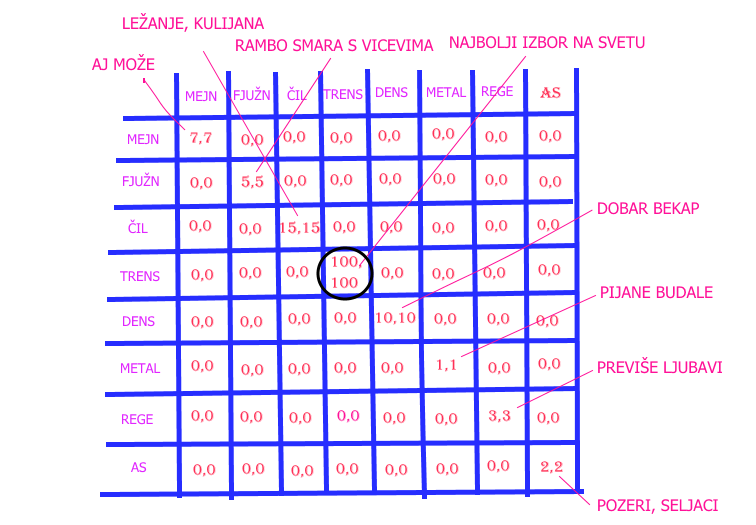
Prokleto bitna stvar u mnogim životnim situacijama, na primer kad se treba naći s nekim na festivalskoj gužvi a mreže pukle pa su mobilni beskorisni. Boban i Maja su se razdvojili nakon ulaska na festival jer je pretresač Bobana samo odmerio i propustio dalje a Maji je pretresačica zavlačila ruku u gaće i brus u potrazi za zlom drogom i trkeljisala je 10 minuta, masa ih je preplavila i pogubili su se. Oboje su se zaboli negde na mejnu, odslušali koncert i sledeći korak je bio da se pronađu. Teoretičari igara uvek ovaj problem predstavljaju sa „ili-ili“ kao da je život eto takav da uvek nudi po dve opcije, a pritom jedna bude baš onako obostrano superiorna, i onda sve bude lako. To je donekle opravdano jer ovo ipak treba da shvati i prosečni student ekonomije, dakle ne naročito bistra osoba, te se stoga ne mogu koristiti baš neki opšti slučajevi sa zilion kombinacija. Zato ćemo mi malo da zamastimo.
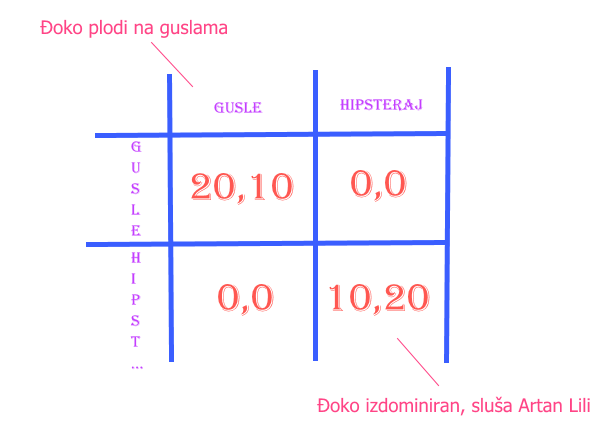
Stvari se komplikuju u trenutku kad želja za pronalaženjem postoji ali su preferencije drugačije (bitka polova). Naravno da je svima jasno da se u tom slučaju na Egzitu možete samo slučajno pronaći, jer jebiga, previše mogućih strategija + alkohol + droga + ležeći britanci čine situaciju nemogućom. Stoga, za igru borba polova valja ispitati nešto jednostavniji slučaj. Đoko Jovov Šimpraga je samo večeras u Beogradu (zbog celovečernjeg koncerta narodnog guslara Đorđija Koprivice, ogranizovanog od strane druženja za očuvanje zavičaja u Kaluđerici) i već ranom zorom mora da se vrati nazad u rodnu grudu (negde u Kordunu, nije tačno locirano). Đoko Jovov Šimpraga se preko neta skontao sa Tinom, hipsterkom lakog morala iz prestonice koja večeras posećuje svirku alternativnog benda (127 lajkova na fejsu i 29 sbskrajbera na jutjubu) u Božidarcu, i cilj je da se sretnu. Međutim, Đoko je telefonom gađao bus plus kontriolora i izgubio telefon tako da mu je dogovor sa Tinom onemogućen. S obzirom da imaju jako veliku želju da se nađu, a da su jedina dva mesta gde se mogu sresti Kaluđerica (koja nikako ne odgovara Tini) i Božidarac (gde bi Đoko lasno mogao ispustiti kršnu kordunsku dušu) mora da postoji određeni kompromis. Ali ko će da bude taj koji će da ga napravi? Mi cenimo da će Kordunaš ipak biti džentlmen.
Dilema samarićanke
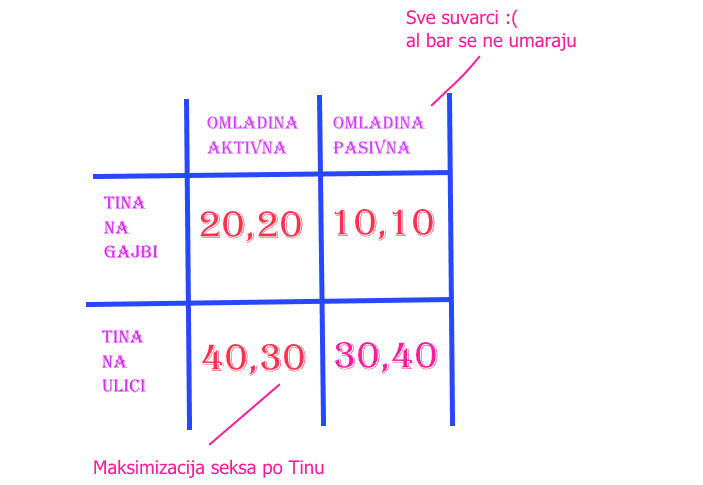
Modifikovana verzija Džejms Bjukenenove (daleki predak Miča Bjukenena) metafore države blagostanja u kojoj se javlja problem sistema podsticaja. Državu blagostanja možemo modelovati ulicom blagostanja (nek bude Kursulina recimo) u kojoj živi već pomenuta Tina, hipsterka lakog morala. Ona, osim nimfomanije, ima i izuzetno izraženu empatiju prema muškarcima, ali joj je teška povreda prednjih ukrštenih elemenata ograničila rejon uticaja samo na ulicu. Tina je sad u dilemi, da li da s bolom šeta ulicom i nudi pomoć ili da sedi kod kuće, uštedi vreme i resurse i čeka potencijalne ljubavnike. Sa druge strane, opuštena omladina koja ne prilazi ribama, pouzdano zna da je Tina u fazonu da sama ište i da ume da pritekne u nevolji, te kontaju da će zadovoljstvo dobiti i iz fotelje.
Kokain vs spid
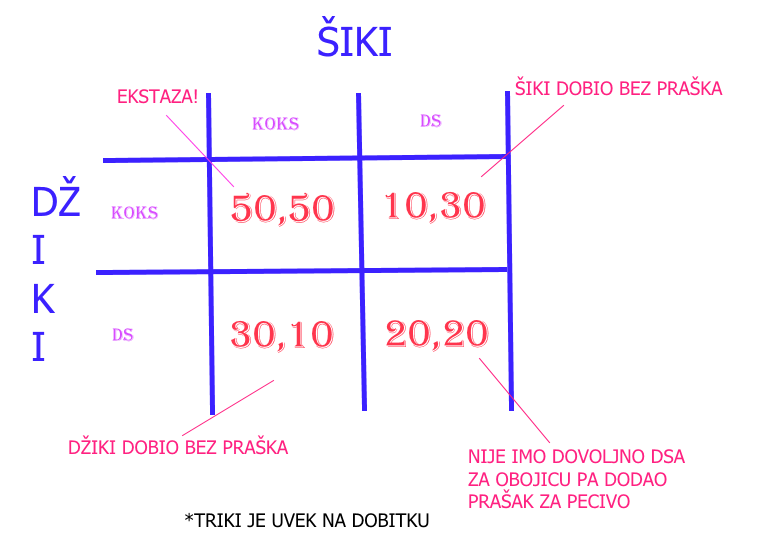
Savremena varijanta lovca na jelene koju je formulisao Žan Žak Ruso. Dva takmičara mogu da biraju da li da saradnjom (koja je nesigurna jer ne znaju 100 posto potez ovog drugog) dođu do boljeg rezultata ili da svako pojedinačno u svojoj režiji dođe do slabijeg ali sigurnog rezultata. Na primer, Šiki i Džiki su dva kretena iz kraja koji su uštekali po 50 evra. Lokalni lerdi Triki im nudi 2 grama kokaniđe za 100 evra (dakle, ako udruže snage, ima da se voznesu do neba), iako singl gram ceni za 75. Pošto su i Šiki i Džiki teški bolidi, pritom veoma nepoverljivi a i vole ponekad da sjebu jedan dugog iz čiste zajebancije, mogu da igraju na siguricu – da svako proba da za svojih 50 evra uzme od Trikija desetku spida sečenog paracematolom, grizom, limuntusom i konjskom spermom u prahu i da se uneredi ko budala. Dakle, da li imati poverenja zarad većeg dobra uz mogućnost da u slučaju ispale jednog ovaj drugi ne bude imao ni za gram (Triki ne prodaje polutke i kvotere) koksa ili sjebati ortaka? Kokain vs spid igru ne treba mešati sa Dilemom zatvorenika, ovde je smisao kooperacija, a to što su Šiki i Džiki maloumnici, to je samo primer slučaja koji se često pojavljuje. Ma, prečesto, da se ne lažemo.
U principu, u teorijama igara, bile one kooperativne ili nekooperativne (a o njima u sledećem tekstu) sve se svodi na anticipiranje narednih koraka i nalaženje najlogičnijeg mogućeg rešenja. Iz čisto ljudske prirode, razlike u shvatanju logike, fokalna tačka se uvek izgubi pa se i jednostavno proste stvari zakomplikuju. Primera radi, na pitanje da brzo zamisle boju i alatku, 90 posto ispitanika automatski odgovara crveni čekić. Ukoliko neko nudi nagradu dvema osobama ako nezavisno jedan od drugog kažu istu kombinaciju boje i alata, mnogo je verovatnije da će rezultati biti ružičasta gedora i pink mistrija nego dva crvena čekiča. Jednostavno, razlika u anticipaciji broja koraka i previd najjednostavnijeg a najboljeg rešenja su jako često u konforntaciji. Na sledećem linku se nalazi jedan sjajan primer o tome koliko je Nešov Ekvilibrijum teže ostvariti ako broj takmičara raste. Zanimljivo da je najlogičniji odgovor dalo svega 5,5 takmičara. Testirajte se.