Teorija igara 2: Ajde da ga merimo, kukavice

Čovek je čoveku vuk čak i kad treba zajedno da sagrade sklonište od vukova u nekoj vukojebini. To smo mogli videti u par primera u prvom tekstu o teoriji igara. Drugi će biti posvećen situacijama kad je bitka za sopstvenu guzicu prvi i jedini cilj.

Papir-kamen-makaze

Iliti rock, paper, scissors, lizard, spock ukoliko ste ljubitelj ne naročito duhovite američke serije o nerdovima. Elementi igre: 3 entiteta od kojih je svaki ponaosob od jednog jači a od jednog slabiji (papir je jači od kamena, kamen od makaza, a makaze od papira). Cilj igre: Naterati protivnika da se uguši u gubitničkim suzama. Naizgled deluje da igra nema niti jednog faktora osim čiste sreće, međutim, ukoliko se igra na više dobijenih runda, određena taktika može značajno da uveća šanse za pobedu.

Kineski matematičar Zhijijan Wang se igrao sa svojim studentima (bolje reći eksperimentisao na njima)  i tražio empirijski dokaz za najbolju taktiku u ovoj igri. Premda je broj pojavljivanja svake konfiguracije bio približan njihovih prirodnim verovatnoćama učestalosti (1/3), Kinez je izvalio da postoji tendencija da pobednici zadržavaju strategiju a da je gubitnici menjaju u svakom sledećem krugu. Na primer, ako igrač A u prvom krugu izabere makaze, igrač B kamen, pobediće potonji. Pretpostavimo da se obojica na početku povinuju tendenciji da pobednik zadržava strategiju a gubitnik menja, te će u drugom krugu A pokazati papir a B zadržati kamen što će sad rezultirati pobedom A. Ukoliko je A upoznat sa uslovnim refleksom u ovoj igri, mogao bi sad da pretpostavi da će B da promeni  formaciju i time ponovo pobedi. Psihologija takođe kaže da će gubitnik češće posegnuti za onom formacijom od koje je izgubio u prethodnoj rundi, pa bi B sada pokazao papir, što znači da A u ovom slučaju menja svoju taktiku u makaze i ponovo pobeđuje. Pošto se runde odigravaju brzo, dok B skonta obrazac koji je uhvatio A, razlika bi mogla da bude već dovoljno velika u korist A. Međutim, ako B zna da A koristi datu taktiku, mogao bi da odgovori kontra strategijom; kad izgubi menja formaciju u onu koja se nije pojavila u protekloj rundi i tako nadmudri A. Lako se da primetiti da se problem nadmudrivanja svodi na broj koraka unapred koji se razmatraju.

S teorijskog stanovišta, igrač ima najviše šansi za pobedu ukoliko podjednako koristi sve formacije (Nešov ekvilibrijum).

Čiji je veći?

Najbitnije pitanje u istoriji kosmosa. Uzmimo opet Džikija i Šikija, dva ortaka iz prošlog teksta, koji su batalili drogiranje, provalili pravoslavlje i počeli zdrav sportski život – dakle, idu u teretanu 2 puta dnevno, piju steroide i izgledaju kao pokretni šifonjeri. Uz hormonalne poremećaje i upliv ziljavih klinki iz kraja koje padaju na njihova razvijena tela, javlja se i sve veći animozitet između njih dvojice. Iako bi bilo najbolje po zdravlje obojice da prestanu da se kljukaju hemijom, eventualni jednostrani prestanak bilo kog od njih bi ovom drugom dao dodatne poene (bar u tim njihovim idiotskim univerzumima) i povećao integritet u društvu a poraženog naterao da se preseli u Zuce, te stoga obojica nastavljaju istom maršrutom. Inače, ova dva idiota su samo parafraza mnogih bilateralnih državnih odnosa kroz istoriju, tipa SAD – Rusija u pogledu nuklearnog naoružanja.

Igra kukavice

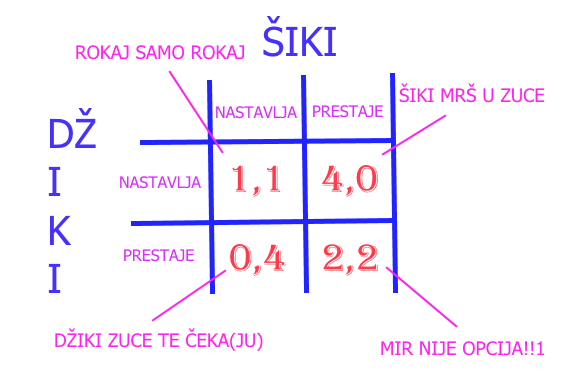
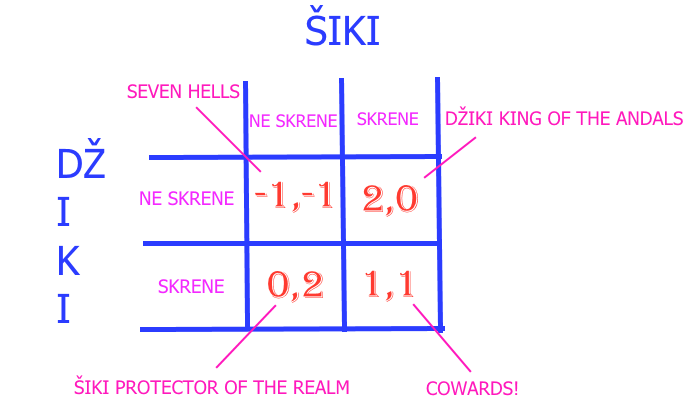
Pošto je čak i idiotima kakvi su Šiki i Džiki jasno da će borba za prevlast u kraju putem bildovanja u teretani da potraje, njih dvojica su rešili da stvar okončaju na relativno jednostavan način – svako će da sedne u svoj auto i jurnuće jedan prema drugom. Ko prvi skrene – kukavica je, gubi sve privilegije u kraju i mora do kraja života da nosi roze flafičaste patofne, a onaj drugi postaje king of the seven kingoms (tačnije, ingerencije su mu u par ulica okolo, al mojne da mu kažete to). Ako obojica idu do kraja, neće preživeti. Ako obojica skrenu, džabe su krečili, kao da se ništa nije desilo, opet moraju u teretanu i da se šibaju steroidima. Šta je rešenje igre ponos vs racio gde je gubitak mnogo veći od dobitka?

Ukoliko Džiki bira da ide do kraja sa verovatnoćom p, onda je za Šikija vrednost čiste strategije bivanja neustrašivim jednaka (-1)*p + 2*(1-p), odnosno 2 – 3p, dok za izbor čiste strategije kukavice dobija 1-p. Sređivanjem jednačina dolazi se do p=1/2, što znači da se Šikiju isplati da bira da ide do kraja ako Džiki ide do kraja sa verovatnoćom manjom od jedne polovine. Ukoliko je Džiki veći hazarder (p>1/2) Šikiju se više isplati da navuče patofne. Naravno, ova Bertrand Raselova varijanta igre kukavice je skoro čisto teorijska jer je u realnom životu gotovo nemoguće dovesti Džikija i Šikija u situaciju da svoje odluke donose na odnosu poznavanje verovatnoće događaja. Stoga je futurista Herman Kan u priču uveo određeni događaj koji značajno menja mogućnost ishoda. U konkretnom primeru vožnje, šta bi se desilo da Šiki par sekundi pre sudara skine volan i baci ga (a da Džiki to primeti), tj ostavi sebi samo jedan izbor?

Dilema zatvorenika

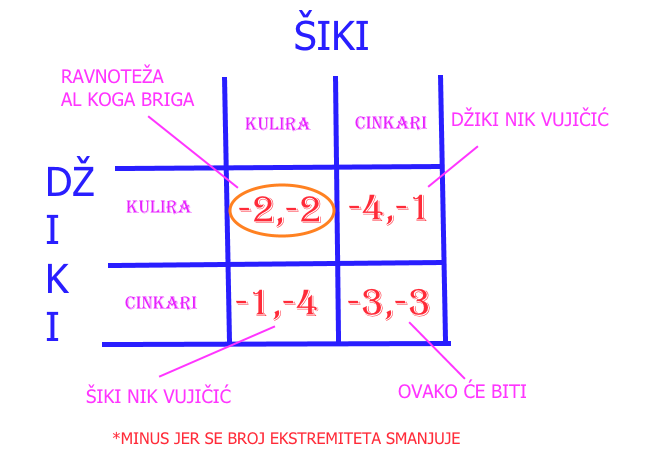
Verovatno najpoznatiji deo o teoriji igara. Govori o tome koliko najbolje individualno rešenje nije i najbolje kolektivno, te stoga odslikava realni svet u pravoj meri. Šiki i Džiki su nekako uspeli da reše situaciju od malopre (nije poznato kako) i nastavili normalnije da žive svoje vašljive živote. Triki (zvezdarski Tuko Salamanka), koga su odrukali, izlazi s robije zbog puštanja u promet opojnih sredstava i željan je osvete. Zarobljava Šikija i Džikija i stavlja svakog u zasebnu prostoriju. Daje im 2 izbora: mogu da ćute ili da cinkare ovog drugog. Ako obojica ćute, polomiće svakom po jednu ruku i jednu nogu. Ako obojica cinkare polomiće svakom po 3 ekstremiteta. Ako jedan ćuti a drugi cinkari, ocinkarenom će biti polomljene obe ruke i obe noge a ovom što cinkari samo leva ruka (Triki je milostiv ali ipak pravedan, a i voli da sluša zvuk lomljena kostiju).

Iako je jedan slomljeni ekstremitet bolje nego dva, dva su  bolje nego tri, a tri svakako bolje nego četiri, rešenje problema uopšte nije tako jednostavno. Pretpostavimo da obojica žele da izbegnu najgoru varijantu u kojoj će ih Triki polomiti naskroz (4 komata), što znači da bi trebalo da cinkare i tako možda prođu najbolje (samo leva ruka) pod uslovom da drugi ćuti, ali s obzirom da svako zna da i ovaj drugi razmišlja tako, onda im ne gine drugo najgore rešenje – tri polomljena ekstremiteta. Dalje, iz te situacije, obojica mogu da skontaju da obostranom promenom strategije mogu da dođu do najmanje lošeg rešenja za njih kao tim, što bi za ovu igru predstavljalo Nešov ekvilibrijum. Ali nakon tog koraka se otvara nova mogućnost; šta ako Šiki pomisli „ok, to je to, siguran sam da je i on došao do toga da je najbolje da ćutimo, jebiga, može nekako da se skakuće na jednoj nozi a levu ruku ionako ne koristimo, tako da kul“ a Džiki ode korak dalje, promeni taktiku i zajebe ga. Mada opet i Šiki može u zadnjem momentu da shvati da ga je Džiki naveo da nasedne i onda ceo proces razmišljanja ispočetka.

Sadista kakav je Triki može zabavu da podigne i na viši nivo ukoliko igru ponovi određen broj puta a da se za konačan ishod računa samo poslednje odigrana igra. To ovoj dvojici unosi još jedan nivo za razmišljanje – rezultate iz prethodnih igara. Ideja vodilja kaže da je u ovom slučaju najbolje sarađivati u prvoj igri a u svakoj sledećoj odigrati kao protivnik u prethodnoj. Kako god teorija rekla, za Šikija i Džikija ne vidim bilo koju drugu opciju osim – ON TE ODRUKAO, NEKA PATI, tj po 3 polomljena ekstremiteta.